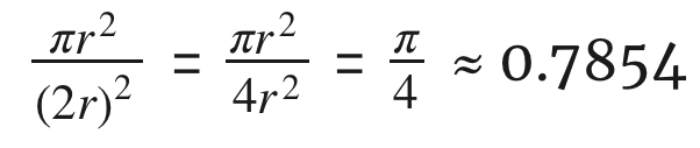As lições de geometria do isolamento social
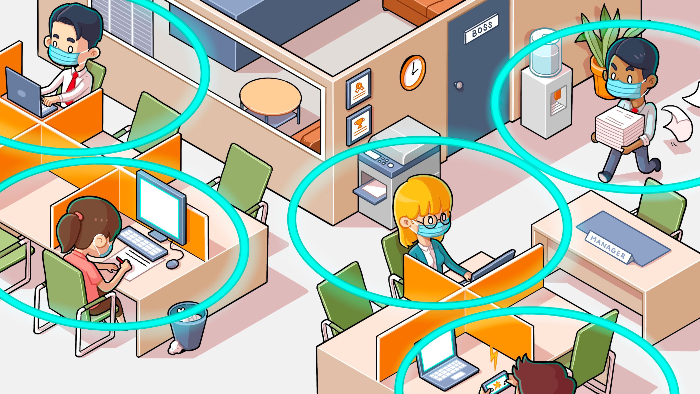
Com a volta de atividades não essenciais em alguns países, milhares de pessoas pelo mundo estão elaborando planos de reabertura segura de escolas, escritórios, transportes e espaços públicos. Como otimizar a ocupação destes locais, levando em consideração a distância mínima de dois metros entre as pessoas? Apesar de ganhar uma nova roupagem, este é um problema antigo na matemática, do qual podemos tirar importantes lições de geometria. Em artigo publicado em julho na Revista Quanta, o matemático Patrick Honner relaciona os planejamentos de reabertura com o estudo do empacotamento de esferas.
“É evidente que há muitos outros fatores no enfrentamento da Covid-19 além da geometria. Mas o estudo do empacotamento de círculos e esferas desempenha uma função importante, assim como na modelagem de estruturas de cristais na química e em espaços abstratos de mensagens na teoria da informação”, explica. Apesar de ser um problema antigo, matemáticos ainda fazem pesquisas que buscam novas descobertas sobre o tema, especialmente nas dimensões mais altas.
Leia mais: Quem foram os primeiros humanos das Américas?
Confira o time que vai representar o Brasil na IMO 2020
Claudio Landim ‘ocupa’ blog de Guga Chacra no Globo
Se a sua tarefa envolve alocar laranjas em uma caixa ou posicionar estudantes a uma distância segura em sala de aula, o tamanho e a forma do seu recipiente são elementos fundamentais para resolver o problema. Para a maioria dos matemáticos, a teoria do empacotamento de esferas tem o objetivo de ocupar o máximo do espaço. Em duas dimensões, isso significa cobrir o plano com círculos do mesmo tamanho que não se sobrepõem.
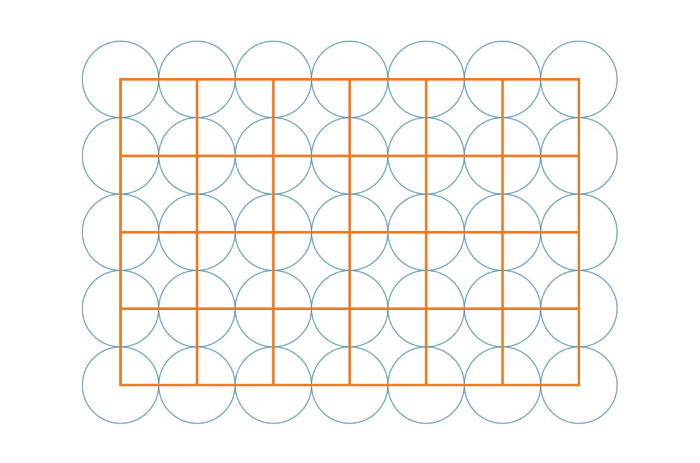
Honner cita como exemplo o método do empacotamento quadrado de esferas, que leva este nome porque podemos imaginar os centros dos círculos como vértices dos quadrados. Como os quadrados cobrem todo o plano de maneira regular, a porcentagem do plano coberto por círculos é igual à porcentagem de qualquer quadrado coberto por círculos.
A simetria deste tipo de agrupamento facilita o cálculo do percentual de círculo que existe em um quadrado. Supondo que cada círculo tenha um raio r, o quadrado teria um comprimento lateral 2r. Como cada um dos quatro vértices do quadrado é coberto por um quarto de círculo, a porcentagem de cada quadrado coberto é apenas a razão da área de um círculo completo com a área de um quadrado:
Portanto, a densidade do empacotamento é de 78.54%. Honner cita ainda outros exemplos de empacotamento de esferas, como a hexagonal, cuja densidade é 90.69%, ainda mais eficiente do que o método quadrado. Ao fim do texto, é possível encontrar uma lista de exercícios que envolvem os conceitos abordados. “Pegue suas laranjas ou suas latas de refrigerante e comece a experimentar. Talvez você é a pessoa que vai preencher estas lacunas”, encoraja Honner.
Confira o artigo na íntegra na Revista Quanta.
Leia também: Com dez equipes, Brasil compete na IMC 2020
Brasileiras participam do Women in Algebraic Geometry